Heaviside step function

The Heaviside step function, or the unit step function, usually denoted by H (but sometimes u or θ), is a discontinuous function whose value is zero for negative argument and one for positive argument. It seldom matters what value is used for H(0), since 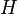is mostly used as a distribution. Some common choices can be seen below.

The function is used in the mathematics of control theory and signal processing to represent a signal that switches on at a specified time and stays switched on indefinitely. It is also used in structural mechanics together with the Dirac delta function to describe different types of structural loads. It was named after the English polymath Oliver Heaviside.

It is the cumulative distribution function of a random variable which is almost surely 0. (See constant random variable.)

The Heaviside function is the integral of the Dirac delta function: H′ = δ. This is sometimes written as

although this expansion may not hold (or even make sense) for x = 0, depending on which formalism one uses to give meaning to integrals involving δ.

Dirac delta function

The Dirac delta function, or δ function, is (informally) a generalized function on the real number line that is zero everywhere except at zero, with an integral of one over the entire real line.^[1][2][3] The delta function is sometimes thought of as an infinitely high, infinitely thin spike at the origin, with total area one under the spike, and physically represents an idealized point mass or point charge.^[4] It was introduced by theoretical physicist Paul Dirac. Dirac explicitly spoke of infinitely great values of his integrand.^[5] In the context of signal processing it is often referred to as the unit impulse symbol (or function).^[6] Its discrete analog is the Kronecker delta function which is usually defined on a finite domain and takes values 0 and 1.

From a purely mathematical viewpoint, the Dirac delta is not strictly a function, because any extended-real function that is equal to zero everywhere but a single point must have total integral zero.^[7] The delta function only makes sense as a mathematical object when it appears inside an integral. While from this perspective the Dirac delta can usually be manipulated as though it were a function, formally it must be defined as a distribution that is also a measure. In many applications, the Dirac delta is regarded as a kind of limit (a weak limit) of a sequence of functions having a tall spike at the origin. The approximating functions of the sequence are thus "approximate" or "nascent" delta functions.