HILBERT TRANSFORM
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u(t), and produces a function, H(u)(t), with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the Riemann–Hilbert problem for holomorphic functions. It is a basic tool in Fourier analysis, and provides a concrete means for realizing the harmonic conjugate of a given function or Fourier series. Furthermore, in harmonic analysis, it is an example of a singular integral operator, and of a Fourier multiplier. The Hilbert transform is also important in the field of signal processing where it is used to derive the analytic representation of a signal u(t).
The Hilbert transform was originally defined for periodic functions, or equivalently for functions on the circle, in which case it is given by convolution with the Hilbert kernel. More commonly, however, the Hilbert transform refers to a convolution with the Cauchy kernel, for functions defined on the real line R (the boundary of the upper half-plane). The Hilbert transform is closely related to the Paley–Wiener theorem, another result relating holomorphic functions in the upper half-plane and Fourier transforms of functions on the real line.
Table of selected Hilbert transforms
Signal |
Hilbert transform[fn 1]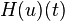 |
|---|---|
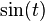 [fn 2] [fn 2] |
 |
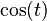 [fn 2] [fn 2] |
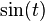 |
 |
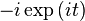 |
 |
 |
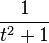 |
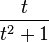 |
Sinc function |
 |
Rectangular function |
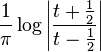 |
Dirac delta function |
 |
Characteristic Function![\chi_{[a,b]}(t) \,](https://upload.wikimedia.org/wikipedia/en/math/4/8/9/48958b1f5fb840c34088bf6a3c9974d4.png) |
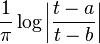 |