CONVOLUTION

In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions, giving the area overlap between the two functions as a function of the amount that one of the original functions is translated. Convolution is similar to cross-correlation. It has applications that include probability, statistics, computer vision, image and signal processing, electrical engineering, and differential equations.

The convolution can be defined for functions on groups other than Euclidean space. In particular, the circular convolution can be defined for periodic functions (that is, functions on the circle), and the discrete convolution can be defined for functions on the set of integers. These generalizations of the convolution have applications in the field of numerical analysis and numerical linear algebra, and in the design and implementation of finite impulse response filters in signal processing.

Computing the inverse of the convolution operation is known as deconvolution.

 
For the usage in formal language theory, see Convolution (computer science).
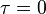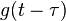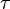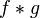Convolution of two square pulses: the resulting waveform is a triangular pulse. One of the functions (in this case g) is first reflected about \tau=0 and then offset by t, making it g(t-\tau). The area under the resulting product gives the convolution at t. The horizontal axis is \tau for f and g, and t for f\ast g.
Convolution of a square pulse (as input signal) with the impulse response of an RC circuit to obtain the output signal waveform. The integral of their product is the area of the yellow region. In both animations the function g is symmetric, and so is unchanged under reflection.