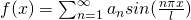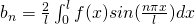FOURIER SERIES
Fourier series is an expansion of a periodic function of period 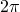 which is representation of a function in a series of sine or cosine such as
which is representation of a function in a series of sine or cosine such as
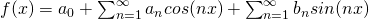
where 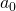 ,
, 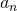 and
and 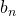 are constants and are known as fourier coefficients.
are constants and are known as fourier coefficients.
In applying fourier theorem for analysis of an complex periodic function , given function must satisfy following condition
(i) It should be single valued
(ii) It should be continuous.
Drichlet’s Conditions(sufficient but not necessary)
When a function 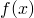 is to be expanded in the interval (a,b)
is to be expanded in the interval (a,b)
(a) 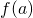 is continous in interval (a,b) except for finite number of finite discontinuties.
is continous in interval (a,b) except for finite number of finite discontinuties.
(b) 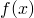 has finite number of maxima and minima in this interval.
has finite number of maxima and minima in this interval.
Orthogonal property of sine and cosine functions
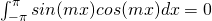
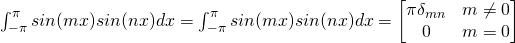
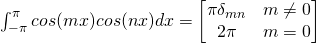
Fourier Constants
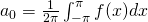
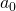 is the average value of function
is the average value of function 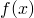 over the interval
over the interval
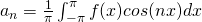
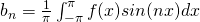
For even functions
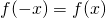 and fourier series becomes
and fourier series becomes
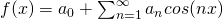
For odd functions
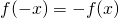 and fourier series becomes
and fourier series becomes
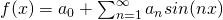
Complex form of fourier series
putting 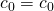
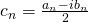
and
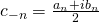
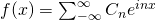
coefficent
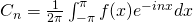
Fourier series in interval (0,T)
General fourier series of a periodic piecewise continous function 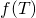 having period
having period 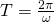 is
is
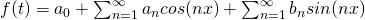
where
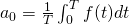
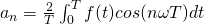
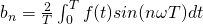
Complex Form of Fourier Series
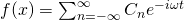
where
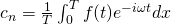
Advantages of Fourier series
1. It can also represent discontinous functions
2. Even and odd functions are conveniently represented as cosine and sine series.
3. Fourier expansion gives no assurance of its validity outside the interval.
Change of interval from 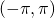 to
to 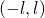
Series will be
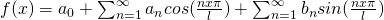
with
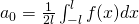
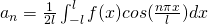
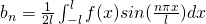
Fourier Series in interval 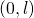
Cosine series when function 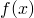 is even
is even
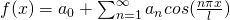
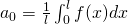
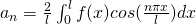
Sine series when function 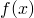 is odd
is odd